A pörgős és szórakoztató társasjáték, a Dobble egyre nagyobb népszerűségnek örvend. Minden korosztály játszhatja, hisz a szabáy nagyon egyszerű: keresd a közös szimbólumot! De hogyan készíthetünk olyan paklit, hogy bármely két lapon pontosan egy minta egyezzen meg?
A játék alapváltozata 55 kártyát tartalmaz, mindegyiken 8 különböző szimbólummal.
Ilyet létrehozni egyszerű: tegyünk minden kártyára például hóembert, és 7 másik, a többi kártyán szereplőktől különböző rajzot! Így 386-féle szimbólummal elérhető, hogy az 55 kártya közül bármely kettőn pontosan egy egyezzen meg. Viszont most nem túl izgalmas a játék: mindig a hóember a közös minta.
Egy másik lehetőség, hogy minden szimbólum pontosan 2 kártyán szerepel, vagyis minden lehetséges pár kártyához egy új mintát használunk. Ez egy jó megoldás lenne, ha csak 8-10 lapot szeretnénk megtervezni. Az 55 lapos paklihoz 1485 különböző szimbólumra lenne szükségünk, és minden kártyán 54 ábrának kellene lennie.
Egy élvezhető játékhoz viszonylag sok kártyát kell készítenünk, mindegyiken viszonylag kevés szimbólummal, minimális számú különböző mintát használva.
Ebben a projektív síkgeometria lehet segítségünkre. Az euklideszi geometriával ellentétben itt nincsenek párhuzamos egyenesek. A projektív geometria axiómái (alapfeltevései):
- bármely két különböző ponthoz pontosan egy egyenes van, amire mindkettő illeszkedik;
- bármely két különböző egyenesnek pontosan egy közös pontja van;
- minden egyenesre legalább 3 pont illeszkedik;
- van 3 pont, ami nem illeszkedik egy egyenesre.
A legkisebb véges projektív sík a Fano-sík, ami 7 pontból és 7 egyenesből áll: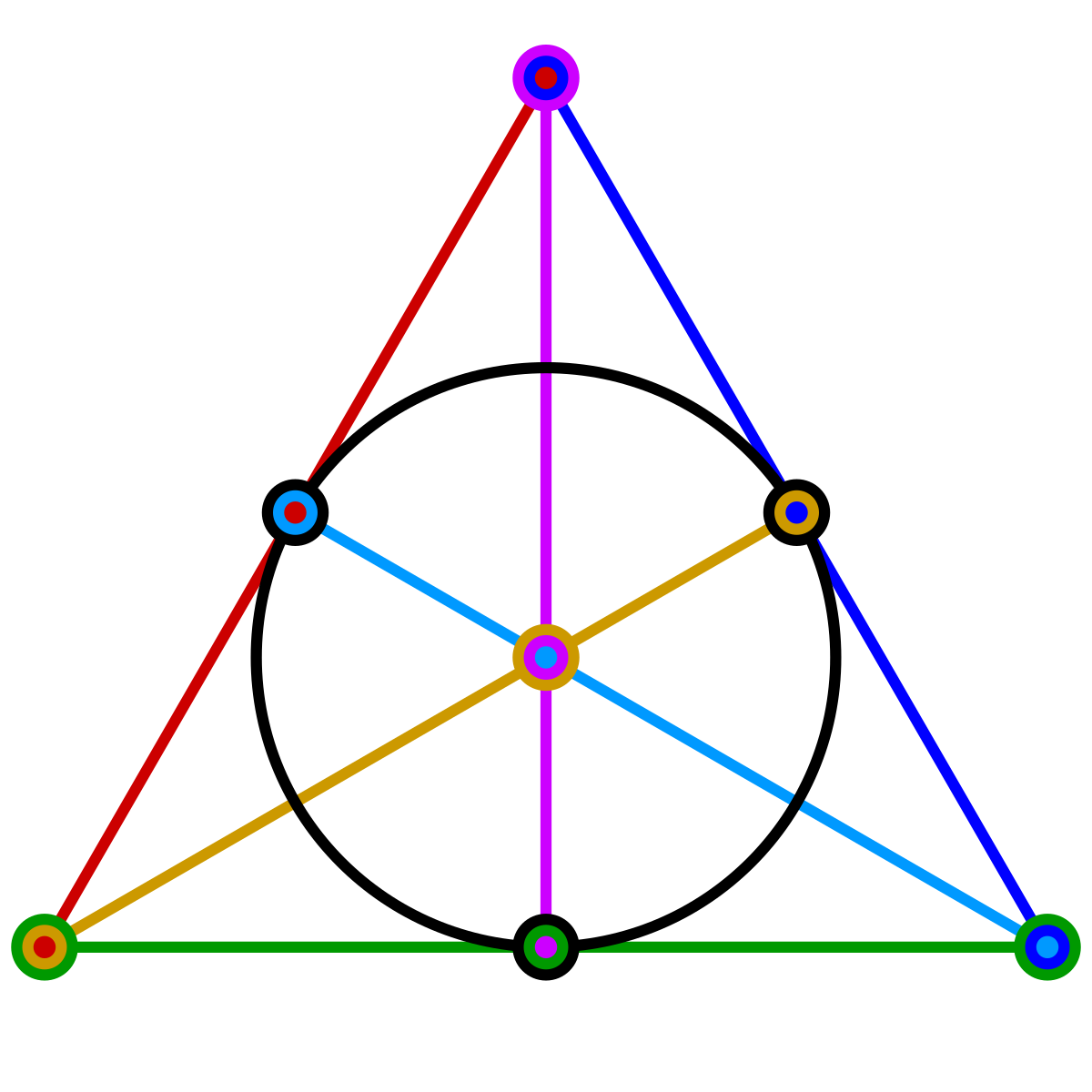
A pontok felelnek meg a játék kártyáinak, az egyenesek pedig az egyes szimbólumoknak. A Fano-sík alapján a játék egy 7 lapból álló verzióját készíthetjük el, amiben minden lapon háromféle rajz szerepel.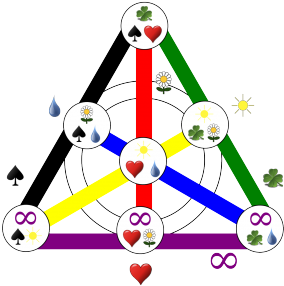
A Fano-sík 2 paraméterű projektív sík. A következő ábrán látható ennek egy másik ábrázolása, és egy 3 paraméterű projektív sík.
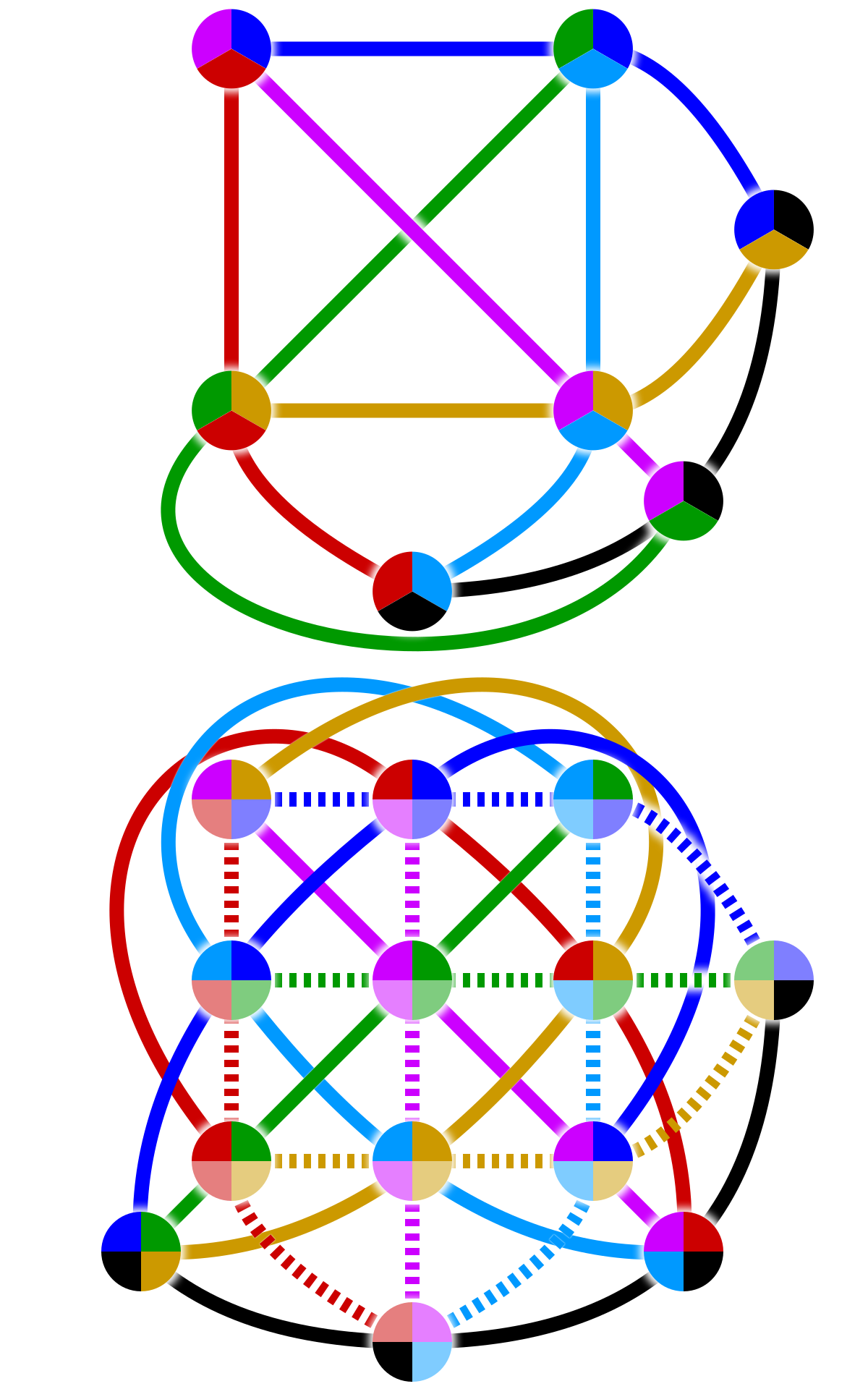
Az n paraméterű projektív sík n²+n+1 pontból és ugyanennyi egyenesből áll. Minden egyenesnek n+1 pontja van, és minden pont n+1 egyenesre illeszkedik. A Dobble játékot a 7 paraméterű projektív síkkal tudjuk modellezni, hisz minden lapon 8 szimbólum szerepel, azaz minden pont 8 egyenesre illeszkedik. Érdekesség, hogy így 57 különböző kártya létezhetne a szabályoknak megfelelően, viszont a játék készítői kettőt kihagytak ezek közül.
Ezek alapján elkészíthetjük a játék akár sokkal nagyobb, és így persze nehezebb változatát is! Ismert, hogy minden prímhatvány fellép egy projektív sík paramétereként, viszont az csak sejtés, hogy csak ilyen szám lehet egy véges projektív sík paramétere.
Ha többet szeretnél hallani a témáról, nézd meg a következő videót!
További információ:
http://www.math.u-szeged.hu/~hajnal/courses/MSc_Halmazrendszerek/MSc_hrsz10/ea13.pdf
