A legújabb tudományos számológépek már számtalan hasznos funkcióval rendelkeznek, rengeteg számítást el tudnak végezni helyettünk. De mennyire bízhatunk bennük? 

Érdekes dolgot kaphatunk, ha a következőt írjuk a számológépbe: 11⁶/13. Ez két egész szám hányadosa, így biztosak lehetünk benne, hogy a megoldás egy racionális szám. A számológép szerint viszont ez π-nek egy racionális számszorosa! Ez viszont tudjuk, hogy nem lehetséges, mivel a π irracionális szám.

Miért kapjuk mégis ezt az eredményt? Egyszerűen azzal magyarázható, hogy a számológépek véges sok számjegyet képesek tárolni, így az irracionális számok közelítő értékeivel tudnak számolni. Az előzőek alapján a számológép a π-t egyenlőnek tekinti a következő kifejezéssel:

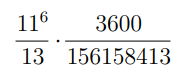
Ez valóban megegyezik a π értékével az első 12 tizedesjegyig, tehát nem tévedett nagyot a gép. Érdekes azonban, hogy más, hasonlóan jó közelítések esetén nem ismeri fel a számológép a π-t. Sőt, a fenti kifejezést beírva sem láthatunk π-t a kijelzőn, más esetben viszont igen! Erről részletesebben a lenti videóban hallhattok.

Bár az előző eredmények valójában kellően pontosak voltak, súlyosabb hibákat is kaphatunk, ha a pontatlan értékkel számolunk tovább.
A  műveletsort beírva a számológép szerint az eredmény 0, pedig láthatjuk, hogy 720-at kellene kapnunk! Ennek a példának a tanulsága, hogy érdemes gondolkodni, mielőtt a számológépre hagyatkozunk.

Még egy érdekes példa:

Ezt beütve a kijelzőn kapott eredmény 1922, vagyis a következő egyenlőséghez jutottunk:

A számológéppel végzett számítások alapján tehát a fenti egyenlőséget igaznak gondolhatjuk, pedig a bal oldal értéke egy páratlan szám, míg a jobb oldal páros! (forrás)

 További érdekes számológépes hibákról olvashattok itt.