Mutatunk egy egyszerű játékot, amiben bármikor legyőzheted a barátaidat, miközben ők azt hiszik, előnyt kapnak!
Van négy dobókockám, de az oldalakon nem a szokásos számok találhatóak:
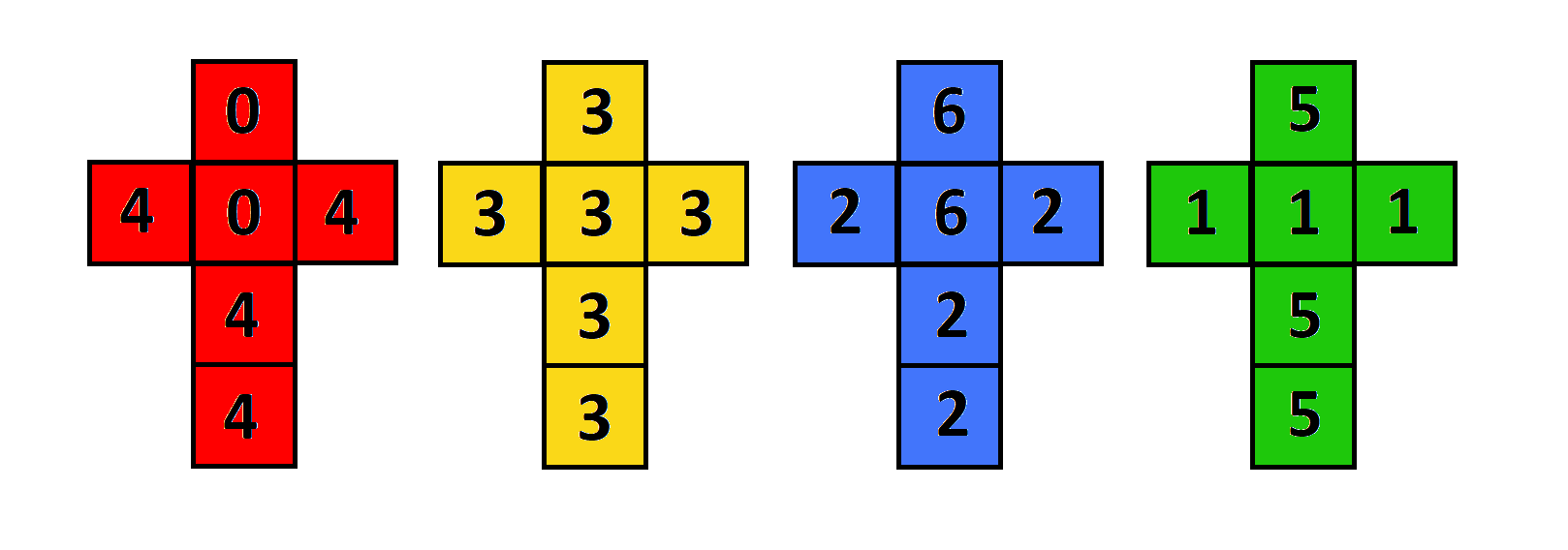
A játék egyszerű: dobunk egy-egy kockával, az nyer, aki nagyobb számot dob. Ezt sokszor megismételjük, mondjuk 100-szor, és az lesz a győztes, aki több kört nyert. Te választhatsz először, bármelyiket a négy kocka közül. De melyik a legjobb kocka? Melyikkel a legnagyobb a nyerés esélye?
A piros kockával játszva 2/3 az esélye, hogy 4-est dobunk, és ekkor legyőzzük a sárga kockát, ami biztosan 3-ast fog mutatni. Tehát a piros és sárga közül a pirosat érdemes választani.
A sárga kockával akkor győzzük le a kéket, ha azzal 2-est dobnak, ami 6-ból 4-szer, tehát az esetek 2/3 részében fordul elő. Ez azt jelenti, hogy a sárga hosszútávon győzedelmeskedik a kék fölött.
Nézzük a kék kockát a zöld ellen. Ha a zölddel 1-est dobnak, a kék mindenképp nyer. Ennek az esélye 50%, azaz 1/2. Viszont a kék úgy is nyerhet, ha a zöldön 5-ös van, a kéken 6-os, ennek az esetnek az esélye 1/2*1/3=1/6. Így annak a valószínűsége, hogy a kék nyer a zöld ellen egy körben, 1/2+1/6=2/3, így ha sokszor dobunk, egyre biztosabb, hogy a kék nyer.
Tehát a piros legyőzi a sárgát, a sárga legyőzi a kéket, a kék legyőzi a zöldet. Ezek szerint a pirosat érdemes választani! Vagy mégsem? Mondhatjuk, hogy a piros a legjobb kocka?
Nem. A zöld legyőzi a pirosat! Gondoljuk meg, 5-össel mindenképp nyer, viszont 1-essel is nyerhet, ha a pirossal 0-t dobnak. Az előzőhöz hasonlóan 2/3 eséllyel a zölddel nagyobb számot dobunk, mint a pirossal, tehát hosszútávon a zöld fog nyerni.
Bármelyik kockát választod, tudok úgy választani, hogy én nyerjek (nagy valószínűséggel)!
Meglepő lehet ez az eredmény, mert gyakran természetesnek vesszük, hogy bizonyos dolgok közül meghatározható a legjobb, és fel tudunk állítani egy sorrendet. Például ha A<B és B<C, akkor A<C. Ez a tulajdonság a tranzitivitás, ami a fenti játékban a kockák erősségére nézve nem teljesül.
Ez valójában számos játékban előfordul, legismertebb példa erre a kő-papír-olló, hiszen az olló legyőzi a papírt, ami üti a követ, viszont az olló veszít a kővel szemben.
