A matematikát bár a logika irányítja, mégis előfordul sokszor hogy logikátlannak tűnik egy bizonyosság.
Az ilyen furcsaságokból gyűjtöttünk össze véletlenszerűen néhányat:
 Kezdjük talán a legegyszerűbben bizonyítható, de mégis elgondolkodtató egyenlőséggel:
Kezdjük talán a legegyszerűbben bizonyítható, de mégis elgondolkodtató egyenlőséggel:
0,999999... = 1
Elemi átalakításokat használva megmutatható, hogy az egyenlőség teljesül végtelen tizedes törtre:
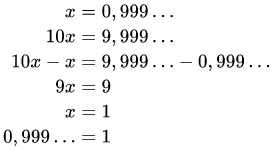
Ennél valamelyest nehezebb belátni azt, hogy a sík ugyan annyi pontból áll, mint a számegyenes.
Ehhez már tudnunk kell azt, hogy két halmazban pontosan ugyan annyi elem van akkor, ha a két halmaz elemeit össze bírjuk párosítani egymással kimaradás és ismétlés nélkül. (Bijekció)
Tegyük ezt meg úgy, hogy az egyenes egy adott pontjának az értékét számjegyenként szedjük szét két számmá:
...0000001234.5678000000..... <==> ...00013.57000... és ...00024.68000...
Könnyű belátni, hogy az ezzel kapott párosítás a sík és a számegyenes minden pontja közt ad párosítást. Tehát minden egyenesbeli ponthoz pontosan egy síkbeli pont tartozik.
Nézzük meg a következő testet:

Ezt a különleges alakot Gábriel harsonájának nevezték el, és az a különleges tulajdonsága, hogy bár a térfogata véges, a felszíne mégis végtelen.
Ez a furcsa tulajdonság magában hordoz egy ún. festési paradoxont:
A harsonát fel tudjuk tölteni festékkel, hiszen véges a térfogata, de lefesteni nem tudjuk, mert végtelen nagy a felszíne.