A 19. században Sam Loyd 1000$ nyereményt ajánlott fel annak, aki meg bírja oldani a 15-ös játékban a 14 és 15-ös elemek felcserélését. Ez már akkor is bizonyítottan lehetetlen volt, viszont egy apró változtatással megoldhatóvá válik.

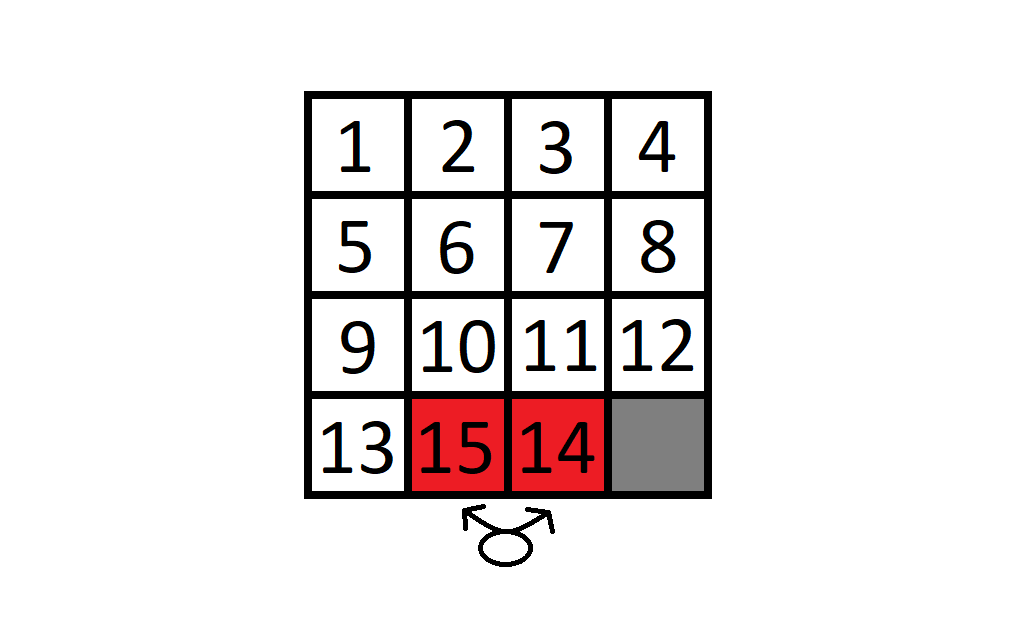
 Ha egy 15-ös játékot el lehetne görbíteni úgy, hogy az első helyet az utolsó hely mellé tegyük,

akkor a lehetetlen állás is megoldhatóvá válik a játékban. Így bárhogyan is lennének a számok összekavarva a mezőkön, a játék biztosan megoldható lenne.

Aki ismeri a bizonyítását a lehetetlen állásnak, az láthatja, hogy így már hiába színeznénk a mezőket pepitában. Az első és az utolsó mező ugyan olyan színt kapna, és egymás mellett lennének. Ez megtöri a paritás problémáját.

 További infó: